[UVA] 108 - Maximum Sum

題目連結

題意:

給你n * m的二維陣列，

找到一個總和最大的矩形，

輸出其總和。

我的作法:

做二維之前，可以先了解一維的O(n)的作法！

這是其他朋友寫的我覺得蠻清楚的可以參考看看哦！

如果已經會一維的了就可以開始做二維的啦

先做出另一個prefix的二維的table：

從第2列開始，將第 i 列的數字 += 第i-1列的數字

以範例測資為例，變成：
0 -2 -7 0
9 0 -13 2
5 1 -17 3
4 9 -17 1

如此一來！利用上面的prefix table的結果，
如果要求如下矩形的和就是= 9 - 0

如果要如下矩形的和就是= -17 - (7)







對於像這樣一豎的數列，你都可以在O(1)求出，
只要知道上界 a 和 下界 b，
就可以利用prefix的表 table[b] - table[a-1]求出該矩形的和，
如果上界是第二列，下界是第三列，
那麼你可以產生一個數列：
(5-0)  (1-(-2))  (-17-(-7))  (3-0)
=  5         3            -10           3
而此數列中的每個元素都是像剛剛那樣用table[3] - table[1]求出

發現了嗎弟弟!
這樣就是一個一維的數列了，
求出最大連續元素和=8，就是在第二列和第三列所組成的高度是2的矩形最大的總和，
也就是
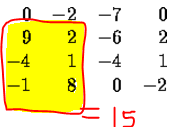
  9  2  -6  2
-4   1  -4  1
這兩列可以組成的矩形中最大的和是8！

再舉一個例子，
上界是第一列，下界是第四列，
可以產生這個數列：
4 9 -17 1
這數列最大連續元素和為13
也就是說
 0 -2 -7  0
 9  2 -6  2
-4  1 -4  1
-1  8  0 -2
高度為4可以組成的矩形中最大的和是13！

所以只要列舉上界和下界就可以知道最大和的矩形了！

--------------------------------------------------

/* 20151102
 * hanting
 * UVa 108 - Maximum Sum
 * C++
 */
#include <iostream>
#include <vector>
using namespace std;
int MaxRectangleSum(vector<vector<int> > &table, int m, int n)
{
    for(int i = 1; i < m; i++)
    {
        for(int j = 0; j < n; j++)
        {
            table[i][j] += table[i-1][j];
        }
    }
    int MaxSum = table[0][0];
    int arr[n];
    for(int low = 0; low < m; low++)
    {
        for(int up = low; up < m; up++)
        {
            if(low)
            {
                arr[0] = table[up][0] - table[low-1][0];
                for(int i = 1; i < n; i++)
                {
                    int tmp = table[up][i] - table[low-1][i];
                    arr[i] = max(arr[i-1]+tmp, tmp);
                    MaxSum = max(MaxSum, arr[i]);
                }
            }
            else
            {
                arr[0] = table[up][0];
                for(int i = 1; i < n; i++)
                {
                    int tmp = table[up][i];
                    arr[i] = max(arr[i-1]+tmp, tmp);
                    MaxSum = max(MaxSum, arr[i]);
                }
            }
        }
    }
    return MaxSum;
}
int main()
{
    int N;
    while(cin >> N)
    {
        vector<vector<int> > table(N,vector<int>(N));
        for(int i = 0; i < N; i++)
        {
            for(int j = 0; j < N; j++)
            {
                cin >> table[i][j];
            }
        }
        cout << MaxRectangleSum(table, N, N) << endl;;
    }

    return 0;
}